坐标系之间的旋转平移变换与对应变换矩阵的关系

1）当绕某根轴旋转时，其他两轴建立的2D坐标系应该保证旋转轴的正方向垂直纸面向外（与旋转角正方向定义相关）；2）空间坐标系的旋转关系与各坐标轴的旋转顺序相关；假设两个空间坐标系O-XYZ与O’-X’Y’Z’之间只存在一个坐标轴的旋转，若坐标系O-XYZ绕自身的X轴逆时针转theta之后与坐标系O’-X’Y’Z’重合，空间中某点M在坐标系O-XYZ和O’-X’Y’Z’中的坐标描述存在以下关系：

 

 

 

 

 

 

 

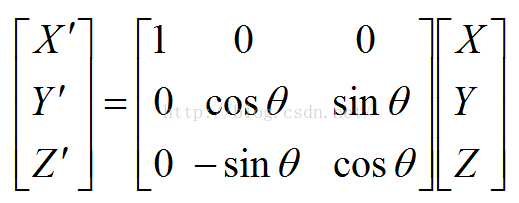
同理，若坐标系O-XYZ绕自身的Y轴或Z轴逆时针转theta之后与坐标系O’-X’Y’Z’重合，则对应的坐标关系如下：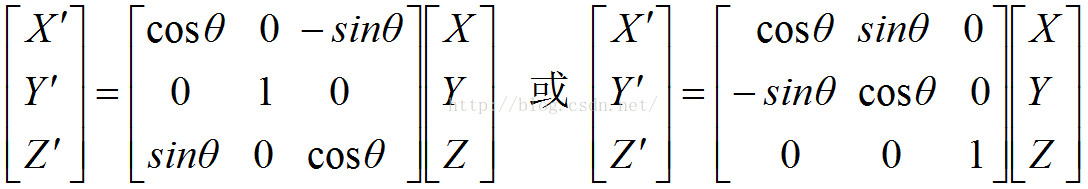

我们注意到，与X和Z轴不同，当绕Y轴逆时针旋转theta角时，对应的旋转矩阵中带负号元素变成了右上角的”sin“元素。原因在于根据上文提到的注意点1）建立的2D坐标系纵轴是X轴，横轴是Z轴，而坐标向量的坐标分量顺序是X,Y,Z，所以得到的X和Z的坐标关系需要调整一下顺序，即可得到上面显示的结果。

可以证明（具体证明过程可以查文献）：对于存在任意旋转变换的两个空间坐标系O-XYZ和O’-X’Y’Z’，可以通过依次绕三个坐标轴旋转一定角度实现两个坐标系对应坐标轴的重合。这里，我们假设坐标系O-XYZ依次绕自身X轴、Y轴、Z轴分别逆时针转theta1，theta2，theta3后可以与坐标系O’-X’Y’Z’重合，则空间中某点M在这两个坐标系中的描述关系如下：

 

 

 

 

 

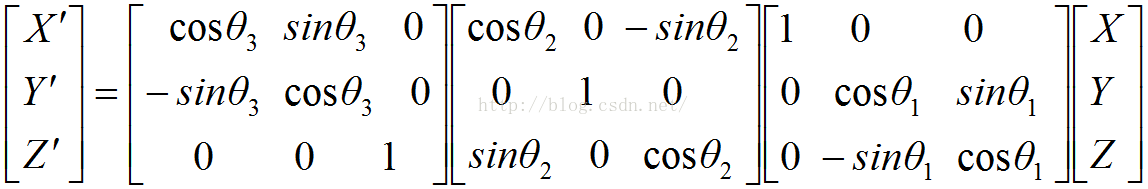
reference：

https://blog.csdn.net/xiaoliu0515_0515/article/details/81413129